线性同余方程

type

status

date

slug

summary

同余

同余的概念

钟表一直是一种同余的形象类比，一个钟表实际上就是把所有整数对12的余数表示了出来（当然这样的话钟表最上面应该是0而不是12）。这样的类比揭示了同余，或者说余数实际上是把所有整数进行了分类，就像钟表把无限的时间分成了12类，接下来通过分类的视角来直观的解释同余是什么。

代数研究分类，数论研究的是整数范围下的分类问题，同余正是一种很重要的分类方式。比如，有些数除以4余1，有些余2，余3等等。那么我们可以将所有的整数分为除4余0，1，2，3的四类，这样的话，4和8都在除4余0的类里面，5和9都在除4余1的类里面，在这样的分类体系下，5，9，13等等数字都是同于意义上等价的，它们相互之间是一种等价关系，所以我们把这样的一个类叫做等价类，特别地，在同于意义上等价的我们可以叫它同余类。但是还有一个问题，“除4余0”这个叫法很麻烦，有什么简单的称呼吗？我们可以在其中挑出一个代表元素，用这个代表元素表示这个同余类或者说这个集合，比如除4余1的数都写成或者直接写成。同时，这样的写法有助于直观理解，比如画个数轴：

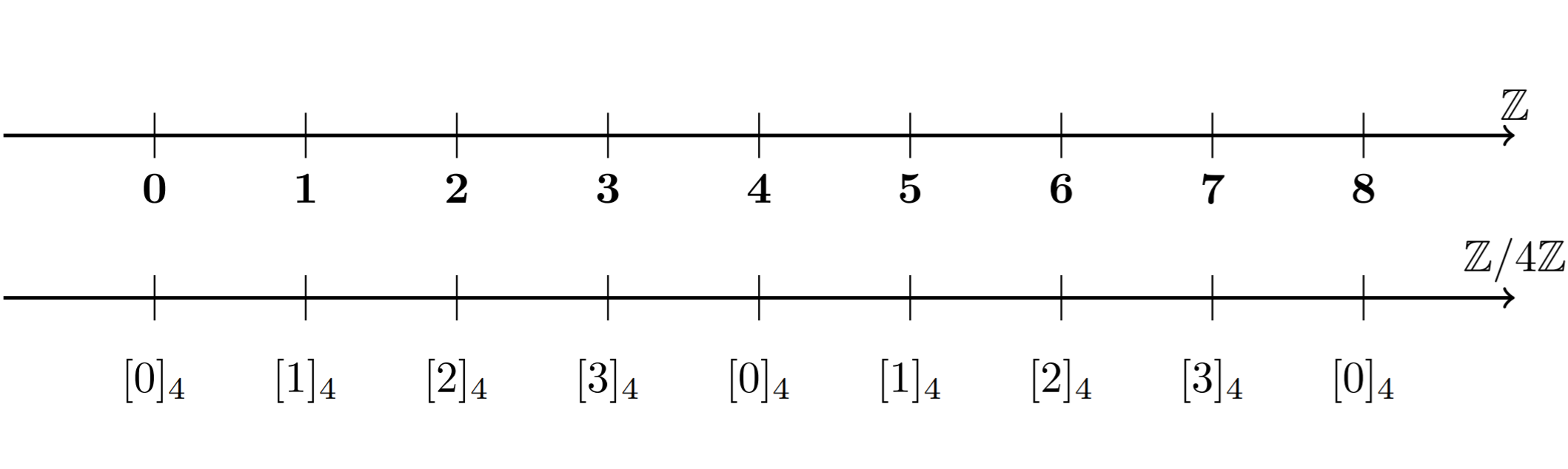
这里的模式就是，每往前走4步就会回到原点，而4步之内都符合整数的性质。

其中符号代表对于模4的同余类，就像代表整数集合一样，我们把模4同余类的代表元素放到一个集合里面，为了方便，称作一个剩余系。特别地，如果所有的代表元素都在这个集合里，那么这个集合称为一个完全剩余系。（非常字面的意思）

同余的性质

一般来说同余符号是这样的：

意思就是a和b除以n的余数是一样的，所以这个式子代表了一种等价关系。当然，它的性质和等号有些相似：这个和等号左右两边加减乘除同一个数的意思是一样的，所以从这个视角来看，我们可以类比出来：

然后当然运算时要注意。

当然还有其它一些性质，可以尝试从上面说的推一推，但也有可能和同余的另一种表示形式有关，也就是：

先理解下这个为什么正确，然后再来看看它的一个应用。

裴蜀定理

裴蜀定理的形式化表达是：

这个定理可以从辗转相除法推出，因为辗转相除法的过程实际上可以看成一系列方程组，而且是线性的。我们可以试着列一下辗转相除法的过程，这里设 y 是较大的数，q 代表商，r 代表余数：

我们总是可以把下面的式子代入到它上面的式子中去，比如把倒数第二个式子中的用最后一个式子中的换掉。这样一直做下去，最后一定能得到一个只包含最后一个余数也就是 r_{k+1} ，以及和的式子。这就是简单版本的裴蜀定理，直观上讲，这个定理指的是的最大公约数是它们的线性组合。

乘法

线性同余方程

形如：

是线性同余方程。

线性指的是未知数的次数为一，同余方程的意思暂且可以理解为原来方程的等号换成了同余记号。

研究一种方程一般的起点是研究有没有解的问题，而线性同余方程的解的存在性问题和有很大的关系。下面先给出结论：

线性同余方程当且仅当时方程有解，且解的数量等于。

证明如下：

首先我们要看出来，同余方程可以写成另外一种形式，也就是，这就和裴蜀定理的结构很像了。

先证明充分性，若则根据裴蜀定理，存在同时乘以得到

只需令即可得到一个解。

再证必要性，如果该方程有解，则存在，而左式能够被整除，因此右式也能被整除，因此得到。